FORM FOUR MATHEMATICS STUDY NOTES TOPIC ONE & TWO

TOPIC 1: COORDINATE GEOMETRY

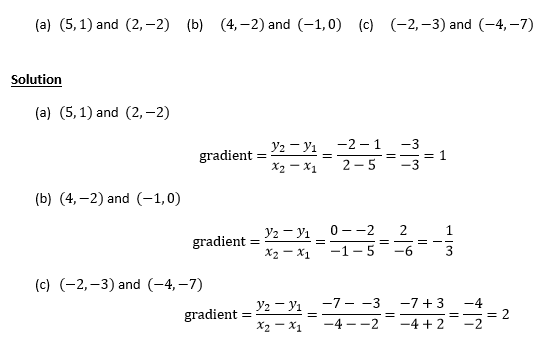
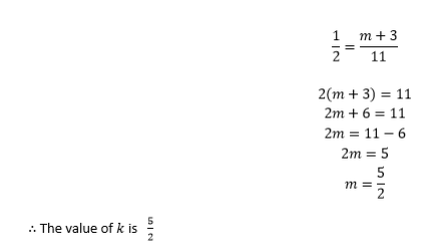
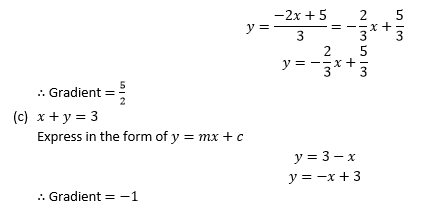
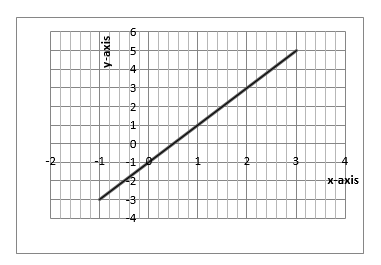
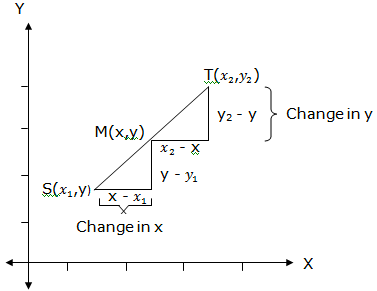
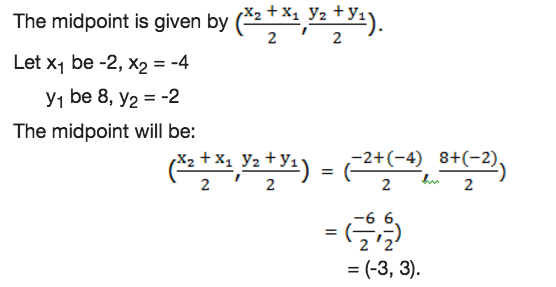
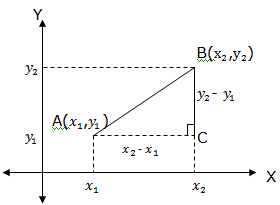
Equation of a Line

The General Equation of a Straight Line

Derive the general equation of a straight line

COORDINATES OF A POINT

•The coordinates of a points - are the values of x and y enclosed by the brackets which are used to describe the position of point in a line in the plane.

The plane is called xy-plane and it has two axis.

1. horizontal axis known as axis and
2. vertical axis known as axis

Consider the xy-plane below

The coordinates of points A, B, C ,D and E are A(2, 3), B(4, 4), C(-3, -1), D(2, -4) and E(1, 0).

Definition

Example 1

Find the gradient of the lines joining

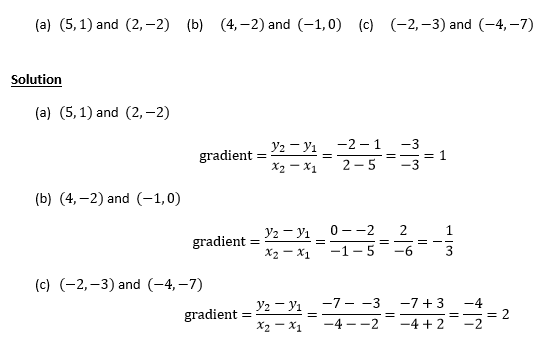
Example 2

(a) The line joining (2, -3) and (k, 5) has a gradient -2. Find k

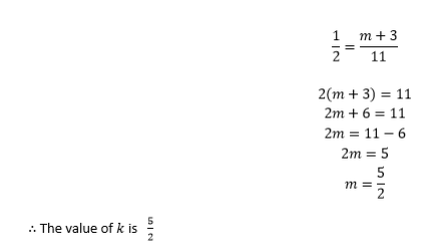
Exercise 1

1. Find the gradientof the line which passes through the following points ;

1. (3,6) and (-2,8)
2. (0,6) and (99,-12)
3. (4,5)and (5,4)

2. A line passes through (3, a) and (4, -2), what is the value of a if the slope of the line is 4?

3. The gradient of the linewhich goes through (4,3) and (-5,k) is 2. Find the value of k.

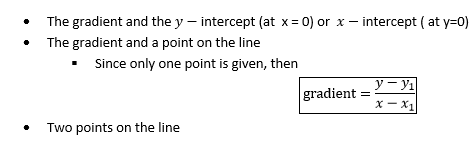
FINDING THE EQUATION OF A STRAIGHT LINE

The equation of a straight line can be determined if one of the following is given:-

Example 3

Find the equation of the line with the following

1. Gradient 2 and intercept
2. Gradient and passing through the point
3. Passing through the points and

Solution

EQUATION OF A STRAIGHT LINE IN DIFFERENT FORMS

The equation of a line can be expressed in two forms

Example 4

Find the gradient of the following lines

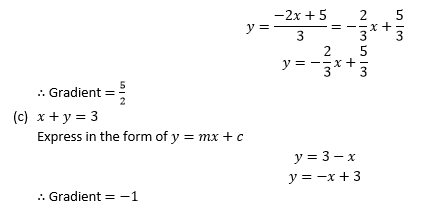
INTERCEPTS

Therefore

Example 5

Find the y-intercept of the following lines

Example 6

Find the x and y-intercept of the following lines

Exercise 2

Attempt the following Questions.

1. Find the y-intercept of the line 3x+2y = 18 .
2. What is the x-intercept of the line passing through (3,3) and (-4,9)?
3. Calculate the slope of the line given by the equation x-3y= 9
4. Find the equation of the straight line with a slope -4 and passing through the point (0,0).
5. Find the equation of the straight line with y-intercept 5 and passing through the point (-4,8).

GRAPHS OF STRAIGHT LINES

The graph of straight line can be drawn by using the following methods;

1. By using intercepts
2. By using the table of values

Example 7

Sketch the graph of Y = 2X - 1

SOLVING SIMULTANEOUS EQUATION BY GRAPHICAL METHOD

• Use the intercepts to plot the straight lines of the simultaneous equations
• The point where the two lines cross each other is the solution to the simultaneous equations

Example 8

Solve the following simultaneous equations by graphical method

Exercise 3

1. Draw the line 4x-2y=7 and 3x+y=7 on the same axis and hence determine their intersection point

2. Find the solutionfor each pair the following simultaneous equations by graphical method;

1. y-x = 3 and 2x+y = 9
2. 3x- 4y=-1 and x+y = 2
3. x = 8 and 2x-3y = 10

Midpoint of a Line Segment

The Coordinates of the Midpoint of a Line Segment

Determine the coordinates of the midpoint of a line segment

Let S be a point with coordinates (x1,y1), T with coordinates (x2,y2) and M with coordinates (x,y) where M is the mid-point of ST. Consider the figure below:

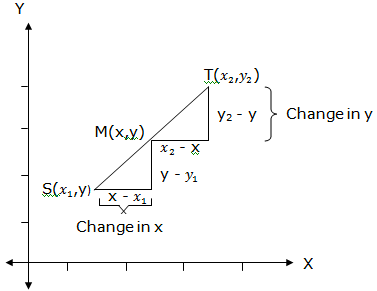
Considering the angles of the triangles SMC and TMD, the triangles SMC and TMD are similar since their equiangular

Example 9

Find the coordinates of the mid-point joining the points (-2,8) and (-4,-2)

Solution

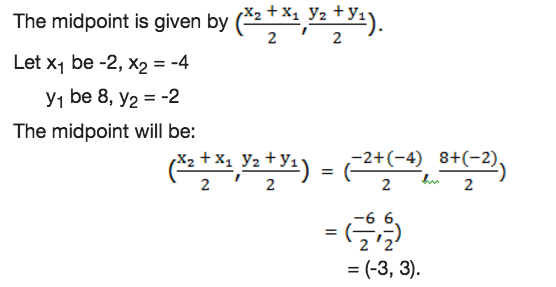
Therefore the coordinates of the midpoint of the line joining the points (-2,8) and (-4, -2) is (-3,3).

Distance Between Two Points on a Plane

The Distance Between Two Points on a Plane

Calculate the distance between two points on a plane

Consider two points, A(x1,y1) and B(x2,y2) as shown in the figure below:

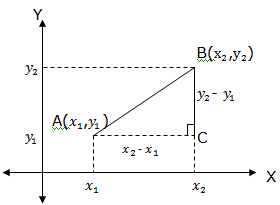
The distance between A and B in terms of x1, y1,x2, and y2can be found as follows:Join AB and draw doted lines as shown in the figure above.

Then, AC = x2– x1and BC = y2– y1

Since the triangle ABC is a right angled, then by applying Pythagoras theorem to the triangle ABC we obtain

Therefore the distance is 13 units.

Parallel and Perpendicular Lines

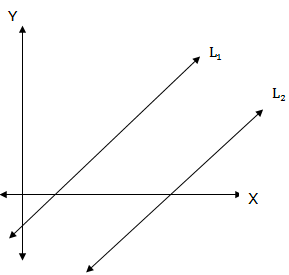
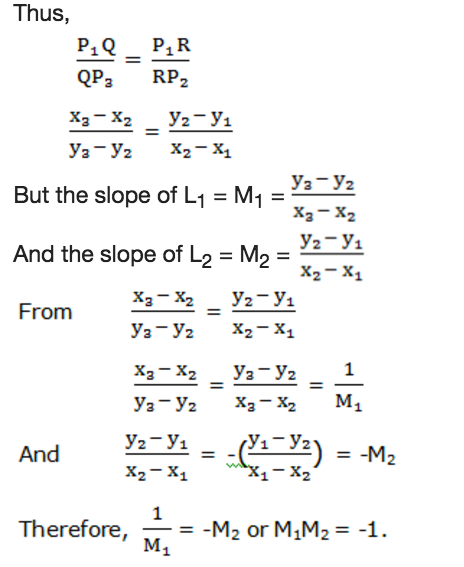
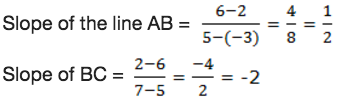
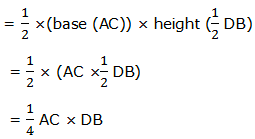
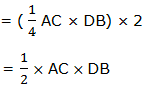
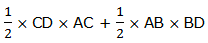
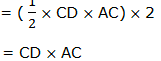
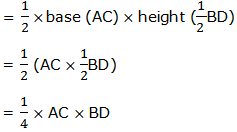
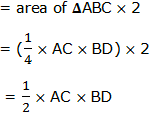
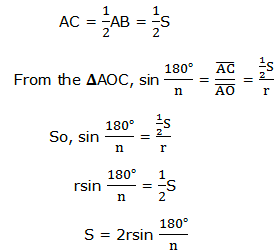
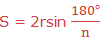
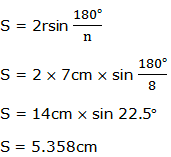
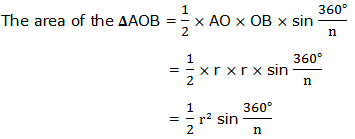
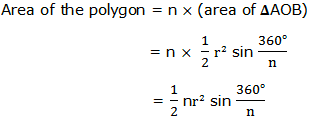
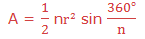
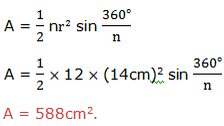
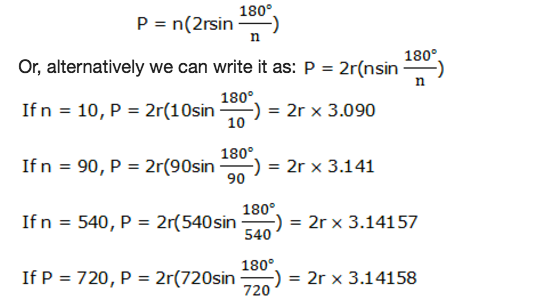
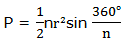
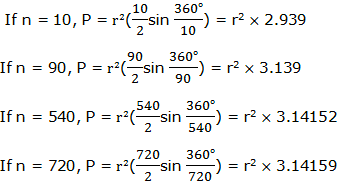
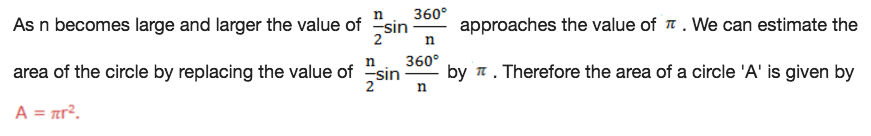
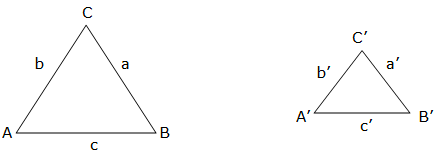
Gradients in order to Determine the Conditions for any Two Lines to be Parallel

Compute gradients in order to determine the conditions for any two lines to be parallel

The two lines which never meet when produced infinitely are called parallel lines. See figure below:

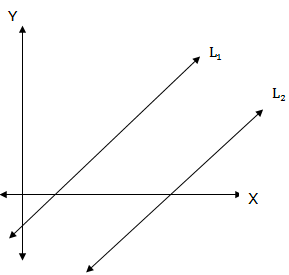
The two parallel lines must have the same slope. That is, if M1is the slope for L1and M2is the slope for L2thenM1= M2

Gradients in order to Determine the Conditions for any Two Lines to be Perpendicular

Compute gradients in order to determine the conditions for any two lines to be perpendicular

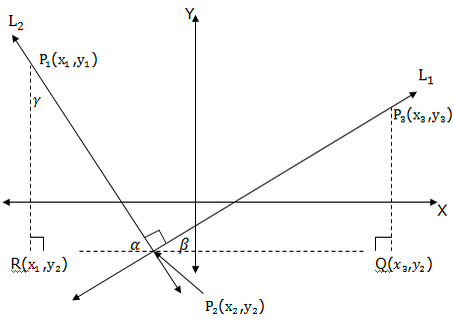
When two straight lines intersect at right angle, we say that the lines are perpendicular lines. See an illustration below.

Consider the points P1(x1,y1), P2(x2,y2), P3(x3,y3), R(x1,y2) and Q(x3,y2) and the anglesα,β,γ(alpha, beta and gamma respectively).

• α+β = 90 (complementary angles)
• α+γ= 90 (complementary angles)
• β = γ (alternate interior angles)

Therefore the triangle P2QP3is similar to triangle P1RP2.

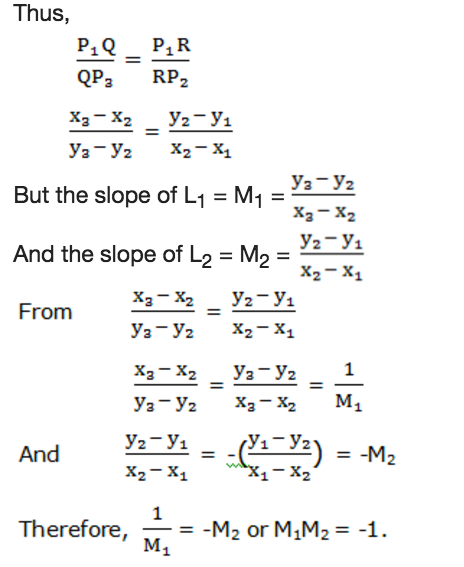
Generally two perpendicular lines L1and L2with slopes M1and M2respectively the product of their slopes is equal to negative one. That is M1M2= -1.

Example 10

Show that A(-3,1), B(1,2), C(0,-1) and D(-4,-2) are vertices of a parallelogram.

Solution

Let us find the slope of the lines AB, DC, AD and BC

We see that each two opposite sides of the parallelogram have equal slope. This means that the two opposite sides are parallel to each other, which is the distinctive feature of the parallelogram. Therefore the given vertices are the vertices of a parallelogram.

Problems on Parallel and Perpendicular Lines

Solve problems on parallel and perpendicular lines

Example 11

Show that A(-3,2), B(5,6) and C(7,2) are vertices of a right angled triangle.

Solution

Right angled triangle has two sides that are perpendicular, they form 90°.We know that the slope of the line is given by: slope = change in y/change in x

Now,

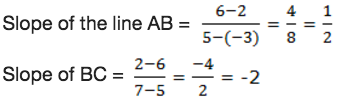
Since the slope of AB and BC are negative reciprocals, then the triangle ABC is a right angled triangle at B.

TOPIC 2: AREA AND PERIMETER

Area of any Triangle

The Formula for the Area of any Triangle

Derive the formula for the area of any triangle

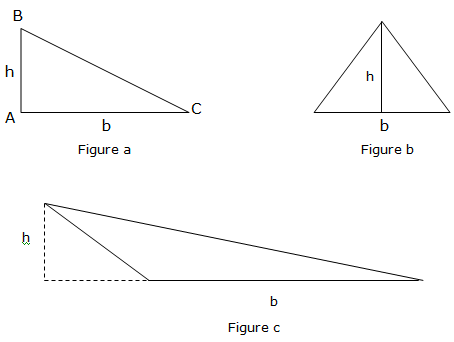
Area of triangle is given by½bh, whereby b is the base of the triangle and h is the height of the given triangle. Consider the illustrations below:

From the figure above, we see where the base and height are located.

Applying the Formula to find the Area of any Triangle

Apply the formula to find the area of any triangle

Example 1

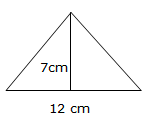
The base of a triangle is 12cm long. If the corresponding height is 7cm, find the area of the triangle.

Solution

Consider the figure below:

The area of a triangle is given by½bh.

Area =½×12cm×7cm

Area = 42cm2

Therefore area of a triangle is 42cm2

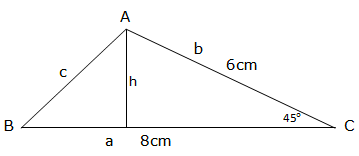
Example 2

The lengths of two sides of a triangle are 6cm and 8cm. Find the area of a triangle if the included is

Solution:

Consider the triangle below, name it triangle ABC.

The area of a triangle above is given by½b×h

So, Area = ½× 8cm× 6cm × sin 45°

=24cm2× sin45°

= 16.97cm2

Therefore the area of ABC = 16.97cm2

Area of a Rhombus

The Formula for Finding the Area of Rhombi in Terms of the Diagonals

Derive the formula for finding the area of rhombi in terms of the diagonals.

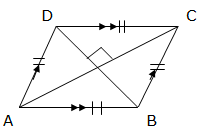
The area of a rhombus is the same as the area of a parallelogram because rhombus is a special kind of parallelogram. Rhombus is a parallelogram with equal sides. Consider the figure below of a rhombus with base b and height h.

So, Area of rhombus = bh

Another formula for finding the area of rhombus can be obtained by using the diagonals. Consider the rhombus below:

Diagonals of a rhombus bisect each other at right angles (means the diagonal lines are half equally), so the area of a rhombus ABCD can be found as follows:

Area of a triangle ABC = area of a triangle ADC

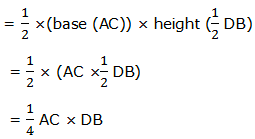
Since the triangles are equal, the area of ABCD:

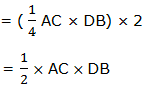
Therefore, the area of a rhombus is equal to half the product of the length of the diagonals.

The Formula to Find the Areas of Quadrilaterals

Apply the formula to find the areas of quadrilaterals

Area of a Trapezium

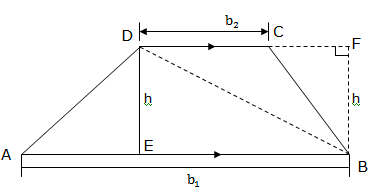
Consider the trapezium with constructed lines as shown in the figure below:

In order to find the area of a trapezium, first let us find the area of the triangles ABD and BDF with the same height h.

The base of the triangle ABD is b1

The base of the triangle BDF is b2

The area of the triangle ABD = ½b1h

The area of the triangle ABE = ½b1h

Area of ABDF =½b1h +½b2h

Area of ABDF=½ (b1 + b2)h

Generally, the area of the trapezium is given by½ (b1+ b2)hor is the product of half the sum of the parallel sides (bases) and the perpendicular distance between them (height)

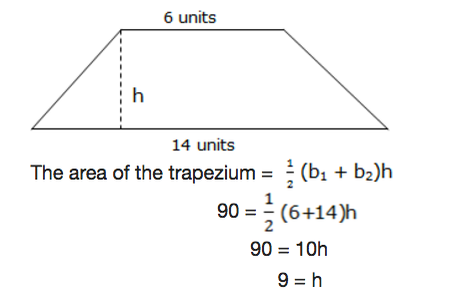
Example 3

Find the height of the trapezium with area 90 square units and bases of 6 units and 14 units

Solution:

Consider the trapezium below:

Therefore the height of the trapezium is 9 units.

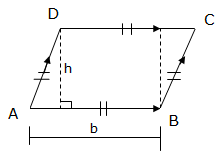
Area of a Parallelogram

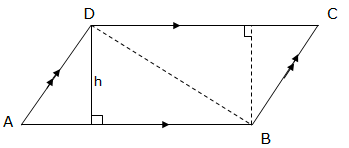
Consider parallelogram below with constructed lines as shown in the figure.

The area of the parallelogram can be formed from the formula for the area of the trapezium. The important thing to note is that the bases for a parallelogram are equal.

Now, the area of the parallelogram ABCD=½ (AB+DC)hsquare units.Since AB = DC

Then, the area of parallelogram ABCD =½ × 2AB × h = AB× h

If AB =b, then Area of the parallelogram ABCD = bh, where b is the base and h is the height of a parallelogram.

Therefore; the area of a parallelogram is equal to the product of the base and the perpendicular height.

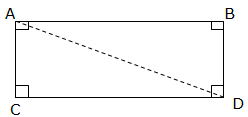
Area of a Rectangle

Consider the rectangle below:

The rectangle ABCD is divided into two congruent triangles, which are triangle ABD and triangle ACD by the diagonal AD.

The area of ABCD = area of triangle ABD + area of triangle ACD

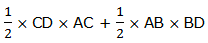
Since the triangles are equal, the area of ABCD is equals to double the area of one of the triangles.The area of ABCD

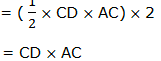
If CD is the length 'l'of the Rectangle and AC is the width 'w' of the Rectangle, then, the area of ABCD = l×w or lw

Therefore, the area of the Rectangle is the product of the length and width.

Area of a Square

A Square is a special rectangle with equal sides. Therefore the area of the square is the product of its lengths. i.e. Area of a square = l × l=l2.

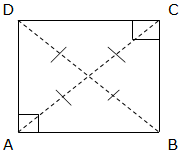
We can also find the area of a square by using the length of the diagonals. Consider the square below with diagonals AC and DB:

Each of the diagonals of a square bisect at a right angle.Area of a triangle ABC = Area of ADC

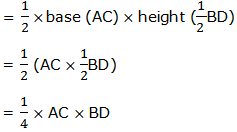
But the area of ABCD

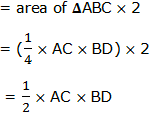
Since the length of the diagonals are equal, then AC = BD.So, the area of ABCD = ½ (AC)2

Therefore the area of a Square is equals to the half of the product of the lengths of the diagonals.

Example 4

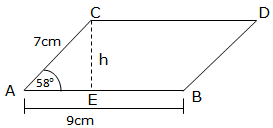
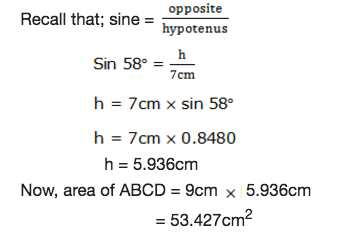
Find the area of a parallelogram ABCD if AC = 7cm, AB = 9cm and the angle ZWX =.

Solution

Area of a parallelogram = base×height

Consider the figure below:

Consider the triangle ACE to find h

Therefore the area of the parallelogram ABCD is 53.427cm2.

Perimeter of a Regular Polygon

The Formula for Finding the Length of a Side of a Regular Polygon

Derive the formula for finding the length of a side of a regular polygon

When we sum up the lengths of the sides of the polygon we obtain what is called perimeter of a polygon. Therefore, perimeter of a regular polygon is the sum of the lengths of the sides of the polygon.

How to find the perimeter of a Regular Polygon inscribed in a circle?

An inscribed polygon is the one whose vertices lie on the circle. If the lengths of the sides of the polygon are the same we say that the polygon is an inscribed Regular Polygon.

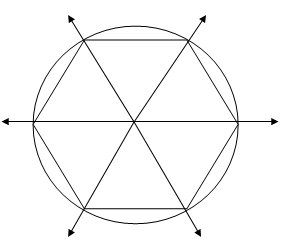
A Regular Polygon with number of sides larger than 2 say n sides can be inscribed in a circle as follows:

For example, if you want to construct an inscribed regular hexagon (6 sides), first draw a circle and locate the center of the circle. Then draw rays that intersect the circle in six points from the center of the circle. Each angle at the center will measure 360°/6 = 60°. Connect the points of intersection on the circle by line segments. The figure formed is an inscribed regular polygon. See the figure below:

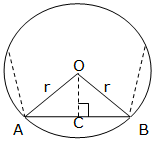
Now, to obtain the formula of finding the perimeter of a regular polygon inscribed in a circle with radius r and center O, let AB be the side of the polygon and OC the perpendicular from O to AB as shown in the figure below:

The angle AOB = 360°/n, since the polygon has n sides.

The angle AOC = the angle AOB and the angle AOB = angle AOC + BOC

Therefore, the angle AOC = ½(360°/n) = 180°/n

Let the length of the side of the regular polygon ABbe S.

Then,

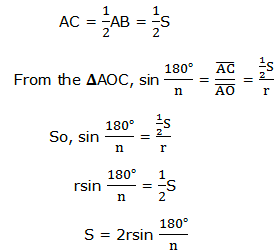
Therefore the length of a regular polygon with n sides inscribed in a circle is given by

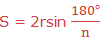
The Perimeter of a Regular Polygon

The formula to determine the perimeter of a regular polygon

If we let 2r = d

From the concept of perimeter that perimeter of a regular polygon is the sum of the lengths of the sides of the polygon , if we have n sides each with length ‘S’ then the sum of the lengths of these sides will be nS. Therefore, Perimeter P of a regular polygon of n sides each with length S is given by:

Example 5

Find the length of one side of eight-sided regular polygon inscribed in a circle with radius 7cm.

Solution

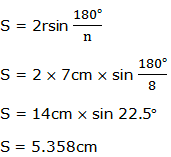
Therefore the length of one side of eight-sided regular polygon with radius of 7cm is 5.358cm

Area of a Regular Polygon

The Formula for Finding the Area of a Regular Polygon

Derive the formula for finding the area of a regular polygon

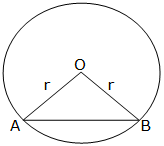
Consider the regular polygon with n sides inscribed in a circle of radius r and center O as shown below:

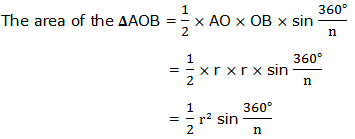
But since each vertex of the polygon is connected to O, the polygon region is divided into n triangles which are equal.

Now,

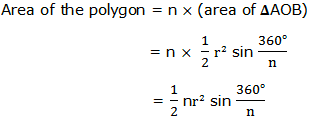
Therefore the area of a polygon of n sides inscribed in a circle of radius r is given by:

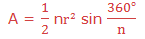
The Formula to Calculate the Area of a Regular Polygon

Apply the formula to calculate the area of a regular polygon

Example 6

Find the area of twelve-sided regular polygon inscribed in a circle of radius 14 cm

Solution

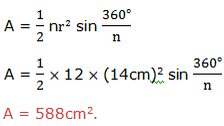
Circumference and area of a circle

Circumference of a circle is the distance around it. Circumference of a circle can be estimated by using a regular polygon with many sides inscribed in a circle with radius r.

We know perimeter of the regular polygon is given by:

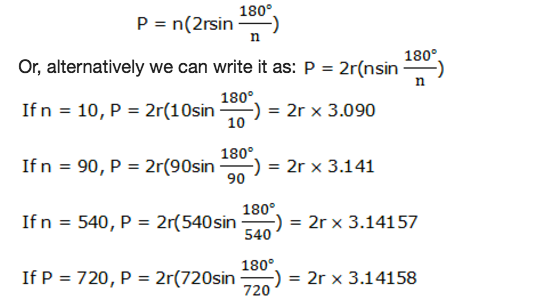
Here we see that, as n increases the value of nsin 180°/napproaches the value ofπ.When n is very large the perimeter of a regular polygon approaches the circumference of the circle. The value ofnsin 180°/ncan be replaced byπbecause it approaches the value ofπwhen n is very large.

Therefore, circumference of the circle C, is given by C = 2πr

Area of a Circle

In similar way we can generate the formula of calculating the area of a circle by considering area of a regular polygon inscribed in a circle of radius r.

We know that, area of a regular polygon is given by:

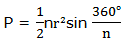
Alternatively we can write it as:

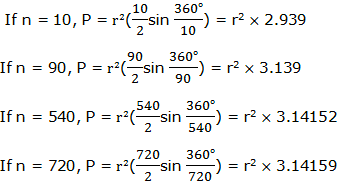
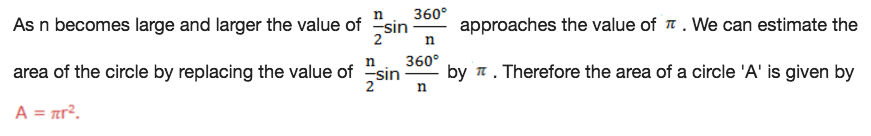
Example 7

Find the circumference of a circle of radius 21cm. (takeπ= 3.14).

Solution

Circumference of a circle, C = 2πr

= 2× 3.14 × 21cm = 131.88cm

Area of Similar Polygons

The Ratio of Areas of Similar Polygons

Find the ratio of areas of similar polygons

Let ABC and A’ B’ C’ be two similar triangles:

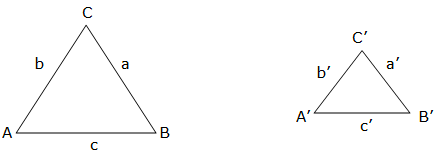
If we find the ratio of their sides we get;

Generally, if the ratio of the lengths of the corresponding sides of two similar polygons is k, then the ratio of their areas is k2.

Problems Related to Ratio for Areas of Similar Polygons

Solve problems related to ratio for areas of similar polygons

Example 8

We are given two triangles which are similar. The length of one side is 8cm and the length of the corresponding side is 14cm. if the area of a smaller triangle is 24cm2find the area of the other triangle.

Solution

Therefore the area of the other triangle is 73.5cm2.

Example 9

The ratio of the areas of two similar polygons is 36:48. The length of a side of the smaller polygon is 10cm. find the length of the corresponding side of the other polygon.

Solution